Polarizace je jednou ze základních charakteristik antén. Nejprve musíme pochopit polarizaci rovinných vln. Poté můžeme diskutovat o hlavních typech polarizace antén.
lineární polarizace
Začneme chápat polarizaci rovinné elektromagnetické vlny.
Planární elektromagnetická (EM) vlna má několik charakteristik. První je, že se energie šíří jedním směrem (ve dvou ortogonálních směrech se pole nemění). Za druhé, elektrické a magnetické pole jsou na sebe kolmé a navzájem ortogonální. Elektrické a magnetické pole jsou kolmá na směr šíření rovinné vlny. Jako příklad uvažujme jednofrekvenční elektrické pole (E pole) dané rovnicí (1). Elektromagnetické pole se šíří ve směru +z. Elektrické pole je směrováno ve směru +x. Magnetické pole je směrováno ve směru +y.
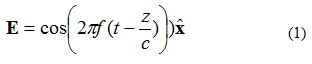
V rovnici (1) si všimněte zápisu: . Jedná se o jednotkový vektor (vektor délky), který říká, že bod elektrického pole leží ve směru osy x. Rovinná vlna je znázorněna na obrázku 1.
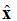
obrázek 1. Grafické znázornění elektrického pole šířícího se ve směru +z.
Polarizace je tvar stopy a šíření (obrys) elektrického pole. Jako příklad uvažujme rovnici elektrického pole rovinné vlny (1). Budeme pozorovat polohu, kde elektrické pole je (X,Y,Z) = (0,0,0) jako funkci času. Amplituda tohoto pole je znázorněna na obrázku 2 v několika časových okamžicích. Pole osciluje na frekvenci „F“.
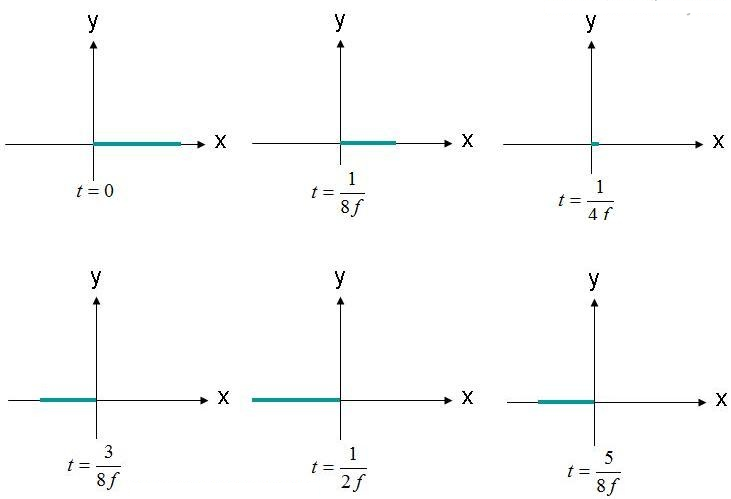
obrázek 2. Pozorujte elektrické pole (X, Y, Z) = (0,0,0) v různých časech.
Elektrické pole je pozorováno v počátku souřadnicového systému a osciluje tam a zpět v amplitudě. Elektrické pole je vždy podél vyznačené osy x. Protože elektrické pole je udržováno podél jedné přímky, lze toto pole považovat za lineárně polarizované. Pokud je osa X rovnoběžná se zemí, lze toto pole popsat také jako horizontálně polarizované. Pokud je pole orientováno podél osy Y, lze vlnu považovat za vertikálně polarizovanou.
Lineárně polarizované vlny nemusí být směrovány podél horizontální nebo vertikální osy. Například vlna elektrického pole s omezením ležícím podél přímky, jak je znázorněno na obrázku 3, by byla také lineárně polarizovaná.
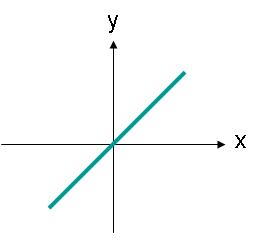
obrázek 3. Amplituda elektrického pole lineárně polarizované vlny, jejíž trajektorie je úhel.
Elektrické pole na obrázku 3 lze popsat rovnicí (2). Nyní existuje složka x a y elektrického pole. Obě složky mají stejnou velikost.
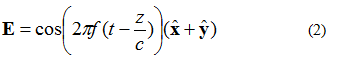
Jedna věc, kterou je třeba si u rovnice (2) všimnout, je složka xy a elektronové pole ve druhé fázi. To znamená, že obě složky mají vždy stejnou amplitudu.
kruhová polarizace
Nyní předpokládejme, že elektrické pole rovinné vlny je dáno rovnicí (3):
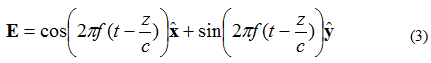
V tomto případě jsou prvky X a Y fázově posunuty o 90 stupňů. Pokud se pole pozoruje jako (X, Y, Z) = (0,0,0) jako předtím, křivka elektrického pole v závislosti na čase se projeví, jak je znázorněno níže na obrázku 4.
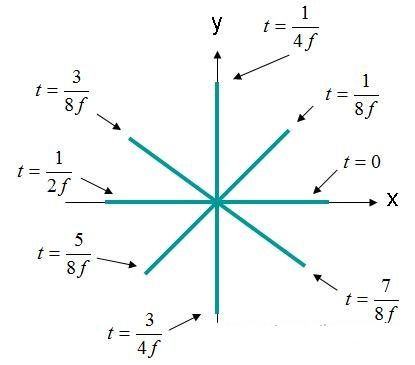
Obrázek 4. Intenzita elektrického pole (X, Y, Z) = (0,0,0) EQ doména. (3).
Elektrické pole na obrázku 4 se otáčí po kruhu. Tento typ pole je popsán jako kruhově polarizovaná vlna. Pro kruhovou polarizaci musí být splněna následující kritéria:
- Standard pro kruhovou polarizaci
- Elektrické pole musí mít dvě ortogonální (kolmé) složky.
- Ortogonální složky elektrického pole musí mít stejné amplitudy.
- Kvadraturní složky musí být fázově posunuty o 90 stupňů.
Pokud se pole pohybuje po obrazovce Wave Figure 4, říká se, že rotace pole je proti směru hodinových ručiček a má pravotočivou kruhovou polarizaci (RHCP). Pokud se pole otáčí ve směru hodinových ručiček, bude mít levotočivou kruhovou polarizaci (LHCP).
Eliptická polarizace
Pokud má elektrické pole dvě kolmé složky, fázově posunuté o 90 stupňů, ale stejné velikosti, bude pole elipticky polarizované. Uvažujme elektrické pole rovinné vlny šířící se ve směru +z, popsané rovnicí (4):
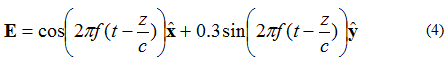
Bod, ve kterém se bude nacházet hrot vektoru elektrického pole, je uveden na obrázku 5.
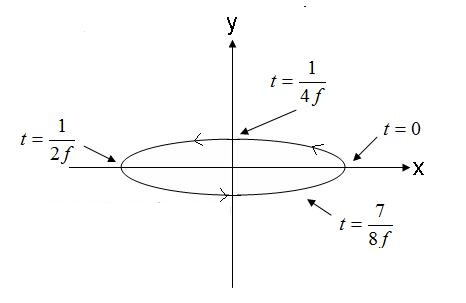
Obrázek 5. Elektrické pole s eliptickou polarizační vlnou. (4).
Pole na obrázku 5, které se šíří proti směru hodinových ručiček, by bylo pravotočivé eliptické, pokud by se šířilo mimo stínítko. Pokud by se vektor elektrického pole otáčil v opačném směru, pole by bylo elipticky polarizované levotočivě.
Eliptická polarizace se dále vztahuje k její excentricitě. Poměr excentricity k amplitudě hlavní a vedlejší osy. Například excentricita vlny z rovnice (4) je 1/0,3 = 3,33. Elipticky polarizované vlny jsou dále popsány směrem hlavní osy. Vlnová rovnice (4) má osu primárně sestávající z osy x. Všimněte si, že hlavní osa může být v libovolném úhlu roviny. Úhel nemusí odpovídat osám X, Y nebo Z. Nakonec je důležité poznamenat, že jak kruhová, tak lineární polarizace jsou speciálními případy eliptické polarizace. 1,0 excentrická elipticky polarizovaná vlna je kruhově polarizovaná vlna. Elipticky polarizované vlny s nekonečnou excentricitou. Lineárně polarizované vlny.
Polarizace antény
Nyní, když si uvědomujeme polarizované elektromagnetické pole rovinných vln, je polarizace antény jednoduše definována.
Polarizace antény Vyhodnocení vzdáleného pole antény, polarizace výsledného vyzařovaného pole. Antény se proto často označují jako „lineárně polarizované“ nebo „pravotočivé kruhově polarizované antény“.
Tato jednoduchá koncepce je důležitá pro anténní komunikaci. Zaprvé, horizontálně polarizovaná anténa nebude komunikovat s vertikálně polarizovanou anténou. Vzhledem k principu reciprocity anténa vysílá a přijímá přesně stejným způsobem. Vertikálně polarizované antény proto vysílají a přijímají vertikálně polarizovaná pole. Pokud se tedy pokusíte přenést vertikálně polarizovanou horizontálně polarizovanou anténu, nebude k dispozici žádný příjem.
V obecném případě, pro dvě lineárně polarizované antény otočené vůči sobě o úhel ( ), bude ztráta výkonu v důsledku tohoto polarizačního nesouladu popsána faktorem polarizačních ztrát (PLF):
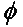
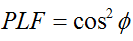
Pokud tedy dvě antény mají stejnou polarizaci, úhel mezi jejich vyzařujícími elektronovými poli je nulový a nedochází ke ztrátě výkonu v důsledku nesouladu polarizace. Pokud je jedna anténa vertikálně polarizována a druhá horizontálně polarizována, úhel je 90 stupňů a nedojde k přenosu žádného výkonu.
POZNÁMKA: Pohybováním telefonu nad hlavou do různých úhlů vysvětlujete, proč se někdy může příjem zlepšit. Antény mobilních telefonů jsou obvykle lineárně polarizované, takže otáčením telefonu se často lze přizpůsobit polarizaci telefonu, a tím zlepšit příjem.
Kruhová polarizace je žádoucí vlastností mnoha antén. Obě antény jsou kruhově polarizované a netrpí ztrátou signálu v důsledku nesouladu polarizace. Antény používané v systémech GPS jsou pravostranné kruhově polarizované.
Nyní předpokládejme, že lineárně polarizovaná anténa přijímá kruhově polarizované vlny. Ekvivalentně předpokládejme, že kruhově polarizovaná anténa se pokouší přijímat lineárně polarizované vlny. Jaký je výsledný faktor ztráty polarizace?
Připomeňme si, že kruhová polarizace jsou ve skutečnosti dvě ortogonální lineárně polarizované vlny, fázově mimo fázi o 90 stupňů. Lineárně polarizovaná (LP) anténa proto bude přijímat pouze fázovou složku kruhově polarizované (CP) vlny. LP anténa proto bude mít ztrátu polarizačního nesouladu 0,5 (-3 dB). To platí bez ohledu na to, o jaký úhel je LP anténa natočena. Proto:
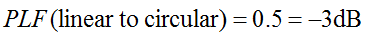
Činitel polarizačních ztrát se někdy označuje jako polarizační účinnost, činitel nesouladu antény nebo činitel příjmu antény. Všechny tyto názvy odkazují na stejný koncept.
Čas zveřejnění: 22. prosince 2023







